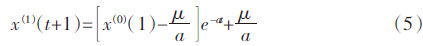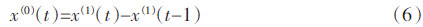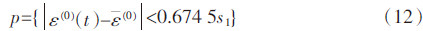土地利用变化与土地资源的规划、管理、保护和利用息息相关，研究土地利用变化可以及时地掌握土地利用的动态，揭示它们的变化规律，为国家制定经济建设的重大决策提供可靠的信息依据^[1]，从而实现土地在国民经济各部门之间的有效配置及利用效率的最大化。

研究土地利用变化需要借助相关数学模型，定量地研究变化的趋势和过程^[2]。目前，国内外学者在土地空间上主要应用的预测数学模型有模拟城市扩张的元胞自动机CA模型^[3]、SLEUTH模型^[4]、神经网络ANN模型^[5]、土地动态模拟的CLUE-S模型^[6]、空间模拟的CA-Markov模型^[7]、土地利用变化的Markov模型^[8]和灰色GM(1，1)^[9]等模型。本文综合考虑各个模型的适用性及优缺点，选择土地利用变化的Markov模型和GM(1，1)模型进行对比预测研究，根据同一数据，分别用2种模型对莱芜市的土地利用变化进行预测，并将所得结果对比分析，以期为莱芜市土地利用规划提供科学依据，以及为土地利用变化研究提供参考。

莱芜市位于泰山东麓，东经117°19′～117°58′，北纬36°02′～36°33′，北邻济南章丘，东临淄博博山和沂源，南临泰安新泰，西邻泰安岱岳区。南北最大距离58 km，东西最大距离56.8 km，面积224 603.43 hm²，人口133.27万。莱芜市辖莱城、钢城2个区，6个街道办事处、14个镇，其中莱城区辖4个街道办事处、11个镇；钢城区辖2个街道办事处、3个镇。

2014年，全市生产总值(GDP)687.60 亿元，比2013年增长8.8%。其中，第一产业增加值53.15 亿元，增长3.6%；第二产业增加值374.78亿元，增长9.7%；第三产业增加值259.67亿元，增长8.1%。3次产业结构由2013年的7.6：56.0：36.4调整为7.7：54.5：37.8。

2014年莱芜市总面积224 603.43 hm²。农用地158 784.02 hm²，占总面积的70.70%，其中耕地72 614.29 hm²、园地16 018.43 hm²、林地37 447.48 hm²、草地32 703.62 hm²；建设用地50 731.84 hm²，占总面积的22.59%，城镇村及工矿用地33 185.56 hm²、交通运输用地6 873.63 hm²、水域及水利设施用地10 672.66 hm²；其他土地15 087.46 hm²，占总面积的6.72%。

Markov模型是一种离散型随机过程运动，具有“无后效性”，即Markov过程的第(n+1)步的状态概率分布与第0，1，2，…，(n-1)步的状态概率分布无关，仅与第n步有关。运用Markov过程需确定土地利用类型之间相互转化的转移概率矩阵P，其数学表达式为^[10]：

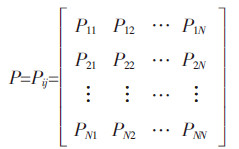
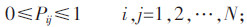
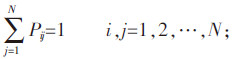
根据Markov性质和条件概率的定义，推导出Markov过程的基本方程：

鐐瑰嚮娴忚鍏紡

Markov过程的基本方程(1)式也可以为：

鐐瑰嚮娴忚鍏紡

根据式(1)，P(n+1)=P(0)P(n+1)。令n趋向于正无穷大，若存在正整数n使P(n)无零元，则Markov过程具有遍历性，遍历性与平稳状态分布存在性互为充要条件，所以存在平稳分布，即极限分布^{[11, 12, 13]}，不管初始状态分布如何，Markov过程的最终都将趋向于平稳分布^{[11, 12]}；但若P(n)存在零元，则Markov过程不具有遍历性，Markov过程的平稳状态分布也不存在^[11]。

数列预测，是对某一指标的发展变化情况所作的预测，其预测的结果是该指标在未来各个时刻的具体数值。而数列预测的基础就是基于累加生成数列的GM(1，1)模型^[10]。

设X⁽⁰⁾={X⁽⁰⁾(1)，X⁽⁰⁾(2)，X⁽⁰⁾(N)}是所要预测的某项指标的原始数据。

如果对{X⁽⁰⁾(t)}_t=1^N作一次累加生成处理，X⁽¹⁾={X⁽¹⁾(1)，X⁽¹⁾(2)，…X⁽¹⁾(N)}，得到一个新的数列{X⁽¹⁾(t)}_t=1^N。这个数列与原始数列相比较，其随机性程度大大弱化，平稳程度大大增加。对于这样的新数列，其变化趋势可以近似地用如下微分方程描述：

鐐瑰嚮娴忚鍏紡

a和μ可以通过如下最小二乘法拟合得到：

鐐瑰嚮娴忚鍏紡

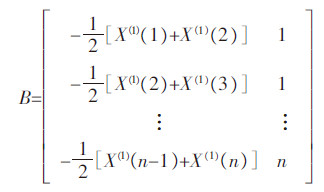
微分方程(3)式所对应的时间响应函数，同样也是数列预测的基础公式：

鐐瑰嚮娴忚鍏紡

由式(4)对一次累加生成数列的预测值x⁽¹⁾(t)可以求得原始数的还原值：

鐐瑰嚮娴忚鍏紡

原始数据的还原值与其观测值之间的残差值ε⁽⁰⁾(t)和相对误差值q(t)如下：

鐐瑰嚮娴忚鍏紡

对于预测公式(5)，是否达到精度要求可按下述方法进行精度检验。首先计算：

鐐瑰嚮娴忚鍏紡

鐐瑰嚮娴忚鍏紡

根据后验比c和小误差概率p对模型进行诊断，当p>0.95和c < 0.35时，认为模型可靠，这时可进行预测^[14]，否则，需要通过对残差序列{ε⁽⁰⁾(t)}_t=2^N的分析对式(5)进行修正^[10]。

根据2009—2010年的变更表，以各土地类型面积占土地总面积比例作为初始概率，可得土地利用初始状态概率分布P(0)。

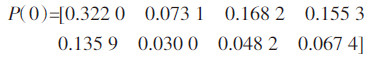
根据莱芜市2009—2014年共5个时间段的土地利用现状变更表，统计出5个时间段内的土地利用转移矩阵并进行平均，可以得出各土地利用类型面积的年平均转化状况，进而计算得2009—2014年5个时间段内各类土地利用类型变化的年平均转移概率矩阵，即初始状态转移概率矩阵(N=0)。

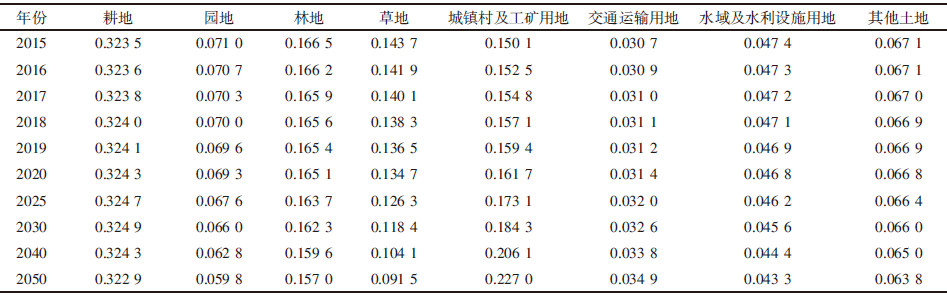
根据之前确定的土地利用的初始状态概率分布P(0)、初始状态转移概率矩阵(N=0)以及Markov过程的基本方程式(1)和式(2)，分别令n=6、7、8、9、10、11、16、21、31、41，利用MATLAB编程^{[12, 15]}运算得2015、2016、2017、2018、2019、2020、2025、2030、2040、2050年的土地利用变化面积比例(表 1)。

表 1 Markov模型预测的各土地类型利用变化的比例 Table 1 Proportion of land use types forecasted by Markov model

表选项

从表 1可以看出，耕地的变化规律是自2015年持续增加至2030年，之后开始减少，与当前我国处在工业化与城镇化中高速发展阶段，耕地需求量巨大的现实有差别，因此，对选取的转移矩阵进行模拟检验。

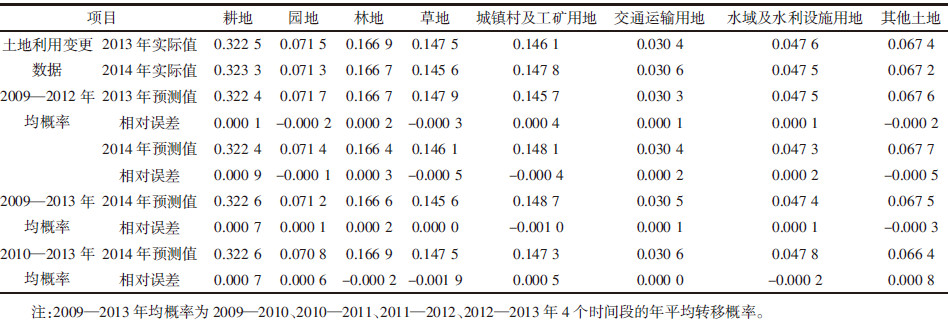
模型预测的关键在于模型预测结果的精准与否，因此需要将预测结果对比实际情况进行精度验证，考虑到土地利用现状变更调查数据的可获取性，在无法获取2009年第二次全国土地调查以前的土地利用现状变更数据的情况下，选取2009年至2013年之间，4个时段中3个以上连续时段的年平均转移矩阵进行组合，根据之前确定的2009年土地利用的初始状态概率分布P(0)，预测2013年和2014年土地利用变化情况，并与实际值进行对比检验(表 2)。

表 2 Markov模型预测精度检验 Table 2 Accuracy test of predictive simulation in Markov model

表选项

从表 2可以看出，误差最小的一次预测为利用2009—2012年均概率的预测，最大相对误差仅为0.000 9，经过计算，仅占2014年实际值的0.277 5%，因此，选取比较具有代表性的2009—2012年均概率，即2009—2010、2010—2011、2011—2012 3个时间段的年平均转移矩阵概率为初始状态转移概率矩阵(表 3)，根据之前确定的2009年土地利用的初始状态概率分布P(0)以及Markov过程的基本方程式(1)和式(2)，再次利用MATLAB编程^{[12, 15]}对2015、2016、2017、2018、2019、2020、2025、2030、2040、2050年的土地利用变化进行预测，结果如表 4所示。

表 3 2009—2012年莱芜市土地利用变化年平均转移概率矩阵 Table 3 Average transition probablity matrix of land use change of Laiwu City from 2009 to 2012

表选项

表 4 Markov模型预测的各土地类型利用变化的比例 Table 4 Proportion of land use types forecasted by Markov model

表选项

根据2009—2014年共5个时间段的土地利用变更数据，统计出2009、2010、2011、2012、2013、2014年共6个年份的统计数据，运用DPS 软件建立GM(1，1)模型：

耕地：x⁽¹⁾(t+1)=-416.273 244e^{-0.325 846t}+484.074 493；

园地：x⁽¹⁾(t+1)=-2 743 182.532 837e^{-0.005 992t}+2 759 594.042 837；

林地：x⁽¹⁾(t+1)=-28 075 397.965 648e^{-0.001 342t}+28 113 166.195 648；

草地：x⁽¹⁾(t+1)=-3 117 233.824 350e^{-0.011 049t}+3 152 120.464 350；

城镇村及工矿用地：x⁽¹⁾(t+1)=2 042 222.325 570^{e0.015 195t}-2 011 701.085 570；

交通运输用地：x⁽¹⁾(t+1)=1 431 794.029 537e^{0.004 693t}-1 425 059.869 537；

水域及水利设施用地：x⁽¹⁾(t+1)=-7 947 439.798 852e-0.001 351t+7 958 254.468 852；

其他用地：x⁽¹⁾(t+1)=-5 140 849.314 118e^{-0.002 975t}+5 155 988.204 118。

根据后验比c和小误差概率p对模型进行诊断，所有8个地类模型都是后验比c < 0.35，小误差概率p>0.95，模型可靠，进行预测，然后计算得各土地类型利用变化比例(表 5)。

表 5 GM(1，1)模型预测的各土地类型利用变化的比例 Table 5 Proportion of land use types forecasted by GM(1，1) model

表选项

从表 5可以看出，耕地的变化规律同第一次Markov模型预测的结果相似，同样是自2015年持续增加，直到2025年，之后开始减少，与当前我国处在工业化与城镇化中高速发展阶段，耕地需求量巨大的现实有差别，因此，同样对选取的元数据进行预测检验。

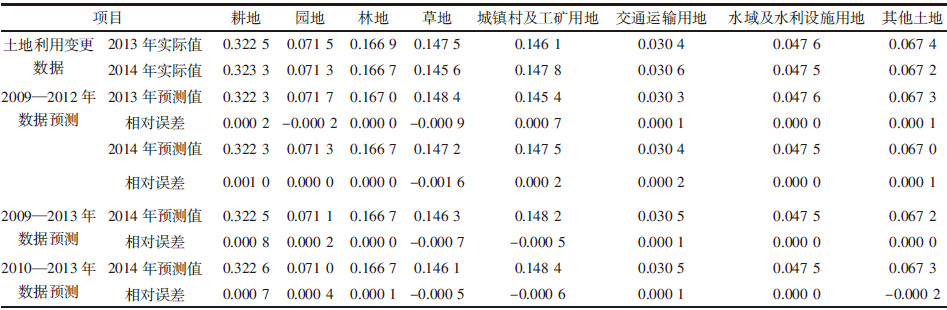
考虑到调查数据的可获取性、与Markov模型预测模型选取数据的统一性以及GM(1，1)对数据的要求，选取2009年至2013年之间，4个时段(5个年份)中4个以上连续年份数据进行组合，预测验证2013年和2014年土地利用变化情况(表 6)。

表 6 GM(1，1)模型预测精度检验 Table 6 Accuracy test of predictive simulation in GM(1，1) model

表选项

误差最小的一次预测取相对误差值占实际值百分比最小的预测，通过对表 6数据的计算，得出误差最小的一次预测为2009—2013的预测，最大误差仅为0.000 8，仅占2014年实际值的0.248 2%，因此，选取比较具有代表性的2009—2013年的数据，即2009、2010、2011、2012、2013年5个连续年份数据，再次运用DPS 软件建立GM(1，1)模型：

耕地：x⁽¹⁾(t+1)=239 174 119.904 077e^{0.000 302t}-239 101 791.804 077；

园地：x⁽¹⁾(t+1)=-2 506 807.732 800e^{-0.006 563t}+2 523 219.242 800；

林地：x⁽¹⁾(t+1)=-27 679 516.401 281e^{-0.001 361t}+27 717 284.631 281；

草地：x⁽¹⁾(t+1)=-3 416 272.965 786e^{-0.010 067t}+3 451 159.605 786；

城镇村及工矿用地：x⁽¹⁾(t+1)=1 950 871.019 808e0.015 890t-1 920 349.779 808；

交通运输用地：x⁽¹⁾(t+1)=1 704 632.195 323e^{0.003 947t}-1 697 898.038 323；

水域及水利设施用地：x⁽¹⁾⁽t+1)=-7 702 702.224 748e^{-0.001 394t}+7 713 516.894 748；

其他用地：x⁽¹⁾(t+1)=-54.678 256e^{-0.650 579t}+68.418 803。

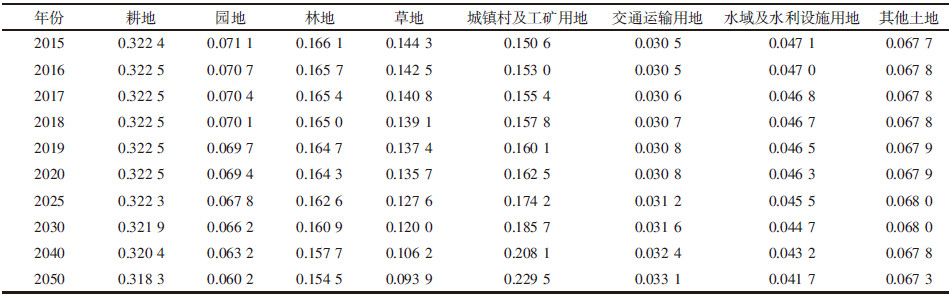
根据后验比c和小误差概率p对模型进行诊断，所有8个地类模型都是后验比c < 0.35，小误差概率p>0.95，模型可靠，然后对2015、2016、2017、2018、2019、2020、2025、2030、2040、2050年的土地利用变化进行预测，然后计算得各土地类型利用变化比例(表 7)。

表 7 GM(1，1)模型预测的各土地类型利用变化的比例 Table 7 Proportion of land use types forecasted by GM(1，1) model

表选项

根据2个模型的土地利用变化预测结果来看(表 4、表 7)：耕地在2015—2020年之间基本保持不变，2020—2050年呈小幅度减少趋势；而园地、林地、草地自始至终都为减少趋势，其中草地的减少幅度最大；城镇村及工矿用地、交通运输用地为增加趋势，其中城镇村及工矿用地增幅最大；水域及水利设施用地、其他土地略有减少，幅度很小。

根据莱芜市2009—2014年共5个时间段、6个年份的土地利用现状变更表数据，统计整理后分别应用Markov模型与GM(1，1)模型进行预测，并将所得结果进行分析，发现其演化趋势与现阶段的实际情况有一定差距，因此，进行时间段内部的数据进行重新组合，对2013年和2014年土地利用变化情况进行预测，对比分析后，选取预测精度最高的数据组合，分别应用Markov模型与GM(1，1)模型对2015—2050年的土地利用变化情况进行预测，得出Markov模型的重新预测各土地类型利用变化的比例(表 4)和GM(1，1)模型的重新预测各土地类型利用变化的比例(表 7)的结果。将两个表格的数据对应相减，得出对比结果见表 8。

表 8 Markov模型与GM(1，1)模型预测值差值 Table 8 Difference of predictive value between Markov model and GM(1，1) model

表选项

分析表 8来看，2020年以前的最大偏差绝对值为2020年其他土地两个模型预测值相减得出的数值，为0.002 1，占2020年Markov预测值的3.048 2%，GM(1，1)预测值的3.144 0%；最大偏差率绝对值为2050年城镇村及工矿用地两个模型预测值相减得出的数值，为0.021 6，占2050年Markov预测值的9.390 0%，GM(1，1)预测值的8.584 0%。

整体上来看，Markov模型的重新预测各土地类型利用变化的比例与GM(1，1)模型的重新预测各土地类型利用变化的比例相似，短期内相应年份预测值吻合度高，各地类变化趋势一致，中长期的预测偏差略大。说明短期内预测结果可信，中长期预测的趋势可作参考。

根据Markov过程的基本方程式(1)和式(2)，令n=100，利用2009—2012年莱芜市土地利用变化年平均转移概率矩阵，经MATLAB编程运算得^{[12, 15]}：P⁽¹⁰⁰⁾存在零元，所以此Markov模型不具有遍历性，又因为遍历性与平稳状态分布存在性互为充要条件^[10]，所以此Markov模型的平稳状态分布不存在^{[11, 12, 13]}。

(1)Markov和GM(1，1)2种预测模型得出各地类变化趋势一致，短期内相应年份预测值吻合度高，中长期的预测偏差略大。说明短期内预测结果可信，中长期预测的趋势可作参考。

(2)耕地在2015—2020年之间基本保持不变，2020—2050年呈小幅度减少趋势；而园地、林地、草地自始至终都为减少趋势，其中草地的减少幅度最大；城镇村及工矿用地、交通运输用地为增加趋势，其中城镇村及工矿用地增幅最大；水域及水利设施用地、其他土地略有减少，幅度很小。

(3)模型局限性与发展。Markov和GM(1，1)2个模型都是在维持现有环境变量与宏观调控政策不变的情况下进行预测，即根据环境变量变化或宏观调控政策产生的已有影响进行深度影响的预测，不能根据宏观的调控政策与制度作出及时地调整与改变，因此，日后有待对可以根据环境变量变化或宏观调控政策进行及时调控的模型做进一步深入的开发与研究。