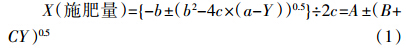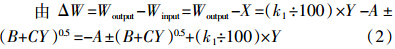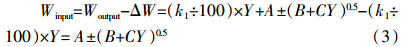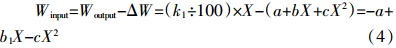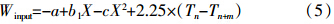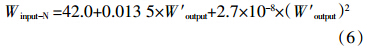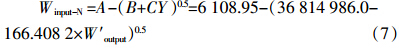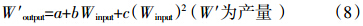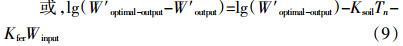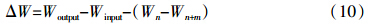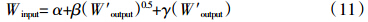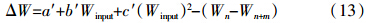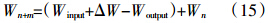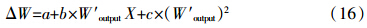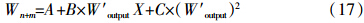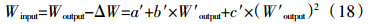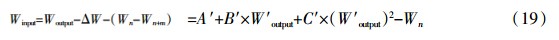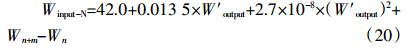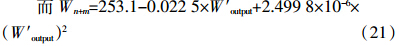文章信息
- 郑宏艳, 刘书田, 侯彦林, 米长虹, 黄治平, 王农, 蔡彦明, 王铄今, 侯显达
- ZHENG Hong-yan, LIU Shu-tian, HOU Yan-lin, MI Chang-hong, HUANG Zhi-ping, WANG Nong, CAI Yan-ming, WANG Shuo-jin, HOU Xian-da
- 生态平衡施肥模型与肥料效应函数模型关系研究
- Relationship of Ecological Balanced Fertilization Model and Fertilizer Effect Function Method
- 农业资源与环境学报, 2014, 31(6): 500-505
- Journal of Agricultural Resources and Environment, 2014, 31(6): 513-520
- http://dx.doi.org/10.13254/j.jare.2014.0286
-
文章历史
- 收稿日期:2014-10-23
2. 北京农业信息技术研究中心, 北京 100089;
3. 北京优雅施软件研发服务中心, 北京 100089
2. Beijing Research Center for Information Technology in Agriculture, Beijing 100089, China;
3. Software Development and Service Center of Beijing Yours, Beijing 100089, China
笔者早期在完成测土配方施肥专家系统软件研制过程中,由于生态平衡施肥模型目前尚缺乏施肥参数,因此施肥模型仍以目标产量模型为基础[1],在软件完成后施肥参数试调过程中,无论如何也不能达到预期的目标,即便是完全模拟的参数也无法实现准确预测施肥量的目的。带着这一重大理论问题进行研究,最后应用生态平衡施肥模型理论及其特征参数求解方法实现了生态平衡施肥模型在方法研究上的重要进展,解决了施肥专家系统建立中的施肥模型理论难题,并对现有施肥模型提出了理论和方法性挑战。
笔者根据区域诸多田间试验研究结果,分别配置了吉林省玉米和水稻区域特征参数模型和区域生态平衡施肥模型,它们均属于二次函数[2]。然而,是否所有作物的区域特征参数模型和区域生态平衡施肥模型都服从二次函数或其他统计模型?只有在这一重大理论问题得到证明之后,才能说明生态平衡施肥模型中使用的统计模型是客观规律的必然产物。本文主要介绍生态平衡施肥特征参数模型和生态平衡施肥模型的一般应用表达式的理论推导过程,并对其与肥料效应函数模型的关系进行讨论,最后对区域生态平衡施肥模型建立的程序进行介绍。
1 特征参数模型和生态平衡施肥模型一般应用表达式推导根据生态平衡施肥模型一般表达式:Winput=Woutput-ΔW-(Wn-Wn+m)[3],现假设土壤肥力水平保持平衡状态,即(Wn-Wn+m)≈0,则ΔW=Woutput-Winput=目标产量需要的养分量-经济(或最大或生态)施肥量。设作物百公斤籽粒养分需要量为k1,产量为X,则Woutput=(k1÷100)×X。
肥料效应函数法是21世纪初提出的肥料用量与作物产量之间的统计关系式,它直观、准确,能揭示多元肥料的相互作用,可以求算出理论上达到最高/最佳产量的最高/最佳施肥量。它有多种表示形式,其中有的统计模型中也将土壤有效养分含量、土壤有效养分利用率和肥料养分利用率引入其中,目的是试图克服单纯的统计模型不考虑土壤和肥料养分的弊端[4, 5]。肥料效应函数模型是目前仍被广泛应用的一类施肥模型。关于其模型弊端稍后进行讨论,本文主要借用它的典型表达式,一元二次(单元肥料方程)肥料效益方程,即Y=a+bX+cX2(Y为作物产量,X为某种肥料用量,a、b、c是系数),来推导生态平衡施肥特征参数模型。
因为,Y=a+bX+cX2,从中可以求出:
式(2)是平方根多项式,它实质上是二次多项式的一种变换。有了这种变换就可以实现由产量(Y)求算ΔW的方法。求出ΔW后,就可以得到施肥量预测模型,它仍为平方根多项式,即,
在此强调指出,由于平方根多项式是二次多项式的一种变换,为了便于应用(解平方根多项式比较复杂)和理解(二次函数直观),将文中特征参数模型配成二次函数,用Y=a+bX+cX2表示。当然统计模型的表达方式将根据实验数据的拟合程度而确定,为便于说明,这里暂且用二次函数表示。于是,ΔW=a+bX+cX2,这里X代表产量。
或,
式(5)中,Tn为某地块土壤有效养分实测值,Tn+m为达到某目标产量所需土壤有效养分适宜含量的下限(mg·kg-1);2.25为将土测值换算为kg·hm-2的平均乘数,这里每公顷20 cm耕层按225万kg土壤计算,下同。
模型中系数含义的简要说明:在式(5)中,-a是产量为0时,保持土壤养分平衡条件下所需要的施肥量;b1为随产量增加施肥量线性增加系数;-c为随产量增加施肥量加大系数(符合报酬递减规律);2.25×(Tn-Tn+m)为土壤有效养分含量变化项。
至此,推导出以上生态平衡施肥特征参数模型和生态平衡施肥模型一般应用表达式,并同时回答了参考文献[1]中吉林省玉米和水稻区域特征参数模型和区域生态平衡施肥模型建立的问题,更为重要的是回答了所有作物的区域特征参数模型和区域生态平衡施肥模型都将服从平方根多项式或二次函数式等统计模型的重大理论问题。
以下再以具体实例证明二次函数和平方根多项式施肥模型具有同样的预测功能,其数学理论基础在于平方根多项式是二次多项式(函数)的一种变换,统计模型具有多种表达方式。
参考文献[1]中吉林省玉米氮肥区域施肥模型(二次函数形式)为:
根据本文推导的结果,可将施肥模型表示为平方根多项式,不难得出,两种模型预测的结果完全相同。有关二元肥料、三元肥料的ΔW求解方法基本同一元肥料效应函数模型方法。
预测举例:目标产量12 500 kg·hm-2,施肥量预测结果如下:
Winput-N (二次函数模型)=215.0 kg·hm-2
Winput-N (平方根模型)=215.3 kg·hm-2
2 区域特征参数模型和区域生态平衡施肥模型理论推导以上模型推导证明了所有作物的施肥特征参数和生态平衡施肥模型都服从以二次函数为代表的统计模型,对于单一田间试验可以求出特征参数(ΔW)和施肥量(Winput)随产量(不同肥料处理)变化的关系曲线,从曲线或模型中可以求出经济的(或最大的或生态的)ΔW和Winput。但是,如何利用多个试验结果建立区域特征参数模型和生态平衡施肥模型是又一个必须解决的理论问题。
取一定区域多年多点肥料试验数据进行数学分析,简单的做法是取其平均值,朱兆良等[6]称其为平均适宜施肥(氮)量,利用统计分析对一定区域多年多点肥料效应函数进行分类统计,从而确定(几类)区域肥料效应方程,以提高模型的代表性,使其适应范围更广,这在理论上更为合理,在实践上更为可行[7, 8]。以上两种代表性做法可以认为是区域施肥模型的前身,但都未能从根本上解决肥料效应函数缺乏代表性和由于没有考虑土壤有效养分因素,因而难以应用于不同地块的根本性理论难题。区域生态平衡施肥模型是利用区域多年多点肥料田间试验数据,经过统计分析确定特征参数随产量变化的函数关系,目的是提高特征参数的代表性,即确定特征参数随产量变化的平均变化趋势。它与现有施肥模型或现有区域施肥模型的主要异同点在于:模型原理不同;所使用的施肥参数不同;在利用多年多点试验数据通过统计分析确定施肥参数或方程系数的方法相同;现有区域施肥模型的表达方式仍以统计模型为主,而区域生态平衡施肥模型整体上遵循质量守恒定律,特征参数遵循生物统计学规律,并包括土壤有效养分变化项或平衡项,既可以进行定量预测,也可以根据具体地块的肥力等级、水分条件、质地类型和其他经营管理水平,通过对区域性的特征参数(包括ΔW和Tn+m)进行适当调整或修正,实现将区域施肥模型转化为地块施肥模型的目的,达到半定量施肥预测;现有区域施肥模型参数获得方法复杂,数学方法未能统一,区域生态平衡施肥模型特征参数获得方法简单。
以下进行区域生态平衡施肥模型的理论分析和推导。
设在一定气候条件、土壤类型和耕作制度区域内,设置某作物的一定数量的肥料田间试验,这些肥料田间试验被安排在不同的肥力等级土壤上,以玉米为例,产量范围从4 500~15 000 kg·hm-2,以产量作为肥力指标的综合表现。因此,一般地,如果地块A产量高于地块B,即Woutput-A大于Woutput-B,地块A作物带走的养分将多于地块B,所多余的养分中一部分将来自土壤,一部分将来自肥料,所以可以认为地块A来自土壤的总养分多于地块B来自土壤的总养分,所以,一般情况下,地块A的ΔWA大于地块B的ΔWB。
由众多个按照产量由低到高(相应ΔW也由低到高)排列的地块的数据可以组成一条曲线,该曲线随着产量的增加,ΔW增加,当增加到一定数值后,ΔW增加的速度变慢。这众多个由不同产量地块组成的曲线相当于一个地块不同肥料处理的曲线(但没有曲线下降区),即多个肥力不同的土壤组合可以看作是同一土壤的不同施肥状态。于是,不需过多的数学证明,我们将得到ΔW必将服从某类统计模型(如二次函数)的结论。特别需要指出的是这条曲线上的每一个ΔW都对应着一个经济产量(或最大或生态产量),即ΔW曲线是由不同产量条件下的经济ΔW组成的,因此称为区域特征参数模型,由此产生区域生态平衡施肥模型。 3 生态平衡施肥模型与肥料效应函数模型关系
肥料效应函数模型客观地反映肥料用量与产量关系和肥料报酬递减规律,其一般模型如下:
生态平衡施肥模型特征参数ΔW表达式为:
由方程(8)不难得出:
或利用原始数据通过统计分析获得如下方程:
将方程(8)和方程(12)分别代入方程(10)中得:
由式(10)得:
一般地,Winput、Woutput (W′output)服从以二次函数为代表的统计模型,所以,ΔW、Wn+m和生态平衡施肥模型也服从以二次函数为代表的统计模型。
肥料效应函数施肥模型建立在统计学基础上,在原理上不遵循质量守衡定律,但可以确定最大施肥量和经济施肥量以及可以评价肥料间的相互作用是该方法的最大优点。函数法试验周期长,年份间重复性差,试验工作量大,预测施肥量误差偏大。通过本文分析不难得出结论,肥料效应函数模型(Winput=a+bX+cX2)是生态平衡施肥模型在不考虑土壤养分变化情况下的特例。
在生态平衡施肥模型中,ΔW=a+bX+cX2,Winput=-a+b1X-cX2+2.25×(Tn-Tn+m),它是生态平衡施肥模型的实际应用表达式。多目标性是施肥技术的发展趋势,即施肥必须兼顾产量、品质、成本、土壤培肥、减少面源污染等。当ΔW分别为最大施肥量特征参数、经济施肥量特征参数和生态施肥量特征参数时,Winput分别表现为最大、经济和生态施肥量。当已知ΔW后,施肥量通过一个参数就可以实现预测。ΔW内涵丰富,内容具体,变异小,易于获得,因此施肥量预测准确,施肥模型易于应用。区域施肥模型和地块施肥模型可以满足复合肥生产企业、肥料销售部门和农民等不同层次用户的不同需求。
如果用文字表达,生态平衡(通用)施肥模型=测土施肥模型的合理内核(遵循质量守恒定律)+肥料效应函数模型的合理外壳(遵循生物统计学规律和肥料报酬递减规律)+土壤养分平衡(可持续土地利用方式)=考虑作物养分平衡+考虑肥料养分平衡和成本+考虑土壤养分平衡和肥料面源污染等生态环境问题。
生态平衡施肥模型服从统计模型,这一点在形式上与肥料效应函数模型有相同之处,即它吸收了肥料效应函数模型的合理“外壳”,但生态平衡施肥模型符合质量守恒定律,同时考虑作物、土壤和肥料养分平衡,具有测土推荐施肥模型和肥料效应函数模型的双重功能。肥料效应函数是肥料报酬递减规律的客观表现,是公认的事实,通过上述理论推导和实践验证,目前肥料效应函数模型和目标产量施肥模型的多数研究结果和多数数据均可作为生态平衡施肥模型及其特征参数的数据源,从而在理论和方法上对两大类施肥模型进行了发展和“革新”。 4 生态平衡施肥模型应用程序举例
生态平衡施肥模型应用是多方面的,为便于读者理解,本文仅以吉林省春玉米氮肥田间试验数据为例,说明其应用程序。 4.1 单个肥料田间试验施肥参数确定方法
通过设置不同养分用量等级的肥料田间试验,可以确定每个试验条件下的最佳产量、最佳施肥量与最佳产量相适应的土壤有效养分适宜含量的下限值。
根据方程ΔW=Woutput-Winput-(Wn-Wn+m),可以求算出不同处理条件下的ΔW。
在同一试验条件下建立ΔW和Wn+m与W′output之间的函数关系或通过图解法确定该试验条件下与最佳产量、最佳施肥量相对应的最佳ΔW和Wn+m。
关于Wn+m,进行以下特殊说明:要想达到某个Woutput,必须有某个最低土壤有效养分含量Wn+m作保证;当Wn>Wn+m,意味着土壤肥力超出了理想的Wn+m下限状态,可以减少一些肥料投入(如北方目前有相当数量的土壤还未缺钾);当Wn<Wn+m,意味着土壤肥力尚未达到理想的Wn+m下限状态,需要培肥(有机和无机);当Wn=Wn+m,意味着土壤肥力保持平衡状态,施肥只需要补充Woutput-ΔW之差即可。由此可见,从广义上来看,Wn+m可以认为是某类土壤和肥力等级上的某类作物的土壤有效养分最佳平衡值的下限,并可理解为季前土壤有效养分的最适含量下限,狭义的Wn+m仍然是季后土壤有效养分最佳平衡值。 4.2 区域生态平衡施肥模型的建立
以表 1中的W′output为自变量(与通常的肥料效应方程统计方法相反),分别以求算的最佳ΔW和最佳Wn+m为因变量,可以考虑用二次函数或平方根多项式拟合产量与特征参数之间的统计关系,于是可以获得以下模型:
 |
地块施肥模型:Winput=Woutput-ΔW-(Wn-Wn+m)
4.4 地块施肥模型预测举例吉林省春玉米区域经济施氮模型:
而 所以,表 2表明,区域玉米施氮量在产量变化幅度为:6 000~12 000 kg·hm-2范围内,施氮量变幅为:124.0~207.9 kg·hm-2。这些预测结果与当前该区域获得的多数玉米经济施氮量研究结果非常吻合。按此施肥量施肥,能够使施肥量被控制在一个合理的范围内,达到减低成本、提高施肥经济效益和减少污染和培肥土壤的多重目的。
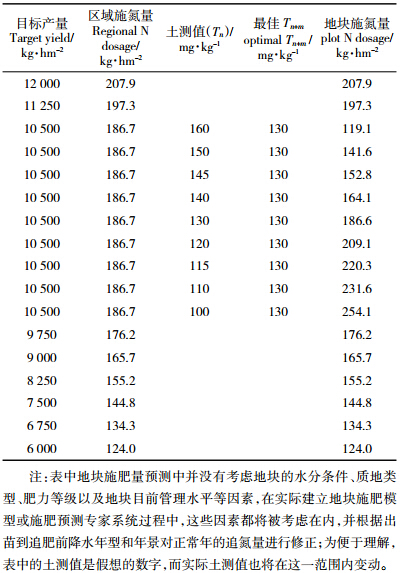 |
当目标产量为10 500 kg·hm-2时,土壤有效氮最佳平衡值低限为130 mg·kg-1,这时如果对该目标产量(平产年配方施肥条件下可以达到的产量标准)的地块进行测土,如果土壤有效氮含量分别为160、150、140、130、120、110、100 mg·kg-1,则所预测的地块施肥量分别为119.1、141.6、164.1、186.6、209.1、231.6、254.1 kg·hm-2。如果以土测值为定量标准,则按区域施肥模型计算的地块施肥量与测土条件下的地块施肥量相比,分别产生百分率偏差为56.8%、31.9%、13.8 %、0%、-10.7%、-19.4%、-26.5%。而实际上当目标产量为10 500 kg·hm-2时,在该地区已经属于高产的中下限水平,土壤有效氮含量一般在110~150 mg·kg-1之间,预测最大偏差在31.9%~-19.4%之间。因此,利用区域施肥模型预测的地块施肥量至少达到了半定量施肥标准。土壤肥力各要素之间是相互影响的,当土壤有效氮含量一般在150 mg·kg-1以上时,目标产量将比10 500 kg·hm-2高;而当土壤有效氮含量小于110 mg·kg-1以下时,目标产量将比10 500 kg·hm-2低。实际上如果将土壤有效氮含量变化范围定为30(115~145) mg·kg-1,足以包含能够达到10 500 kg·hm-2的大多数地块,这时预测最大偏差为22.2%~-15.3%,与测土法预测相比,预测精度约在75%以上。 5 结论和展望
笔者从不同侧面讨论了生态平衡施肥模型与现有2类施肥模型的主要异同点,生态平衡施肥模型是一类新的施肥模型,是值得在理论上、方法上和实际应用效果上进行深入研究的课题。而肥料效应函数模型是生态平衡施肥模型在不考虑土壤有效养分因素情况下的特例;区域生态平衡施肥模型能够满足地块半定量施肥预测的需求。 为促进施肥理论、方法和技术的发展,希望得到国内外同行研究者和兴趣者的共同参与,为此,笔者提出以下题目作为研究重点供读者参考:生态平衡施肥模型理论、方法和试验研究方法的完善;与现有施肥模型的主要异同点;利用现有施肥数据求算特征参数方法研究;区域特征参数模型研究;水肥耦合生态平衡施肥模型及其田间试验方法研究;生态平衡施肥模型长期定位试验研究;特征参数特别是ΔW中各分项参数的试验、求算方法;影响特征参数变异因素研究;特征参数联网研究等等。
| [1] | 黄治平, 米长虹, 侯彦林, 等. 生态平衡施肥模型与目标产量施肥模型比较研究[J]. 农业资源与环境学报, 2014, 31(6): 495-499.HUANG Zhi-ping, MI Chang-hong, HOU Yan-lin, et al. Comparison of target yield method and ecological balanced fertilization model[J]. Journal of Agricultural Resources and Environment, 2014, 31(6): 495-499.(in Chinese) |
| [2] | 侯彦林, 闫晓燕, 任 军, 等. 区域生态平衡施肥模型建立的方法和应用[J]. 土壤通报, 2003, 34(1): 33-35.HOU Yan-lin, YAN Xiao-yan, REN Jun, et al. Establishment method and application of regional ecological balanced fertilization models[J]. Chinese Journal of Soil Science, 2003, 34(1): 33-35.(in Chinese) |
| [3] | 侯彦林. “生态平衡施肥”的理论基础和技术体系[J]. 生态学报, 2000, 20(4): 133-139.HOU Yan-lin.Theory and technological system of ecological balanced fertilization[J]. Acta Ecologica Sinica, 2000, 20(4): 133-139.(in Chinese) |
| [4] | Ghosh P C, Misra U K. Modified Mitscherlich-Bray equation for calculation of crop response to applied phosphamte[J]. Journal of the Indian Society of Soil Science, 1996, 44(4): 786-788. |
| [5] | Bangar A R. Fertilization of sorghum based on modified Mitscherlich-Bray equation under semi-arid tropics[J]. Journal of the Indian Society of Soil Science, 1998, 46(3): 383-391. |
| [6] | 朱兆良, 张绍林, 徐银华. 平均适宜施氮量的含义[J]. 土壤, 1986(6): 316-317.ZHU Zhao-liang, ZHANG Shao-lin, XU Yin-hua. The definition of average suitable amount of nitrogen application[J]. Soils, 1986(6): 316-317.(in Chinese) |
| [7] | 毛达如, 张承东. 多点肥料效应函数的动态聚类方法[J]. 北京农业大学学报, 1991, 17(2): 49-54.MAO Da-ru, ZHANG Cheng-dong. Cluster analysis of quadratic res-sponse fanction on the fertilizer dispersed experiments[J]. Acta Agriculturae Universitatis Pekinensis, 1991, 17(2): 49-54.(in Chinese) |
| [8] | Colwell J D. Development and evaluation of general or transfer models of relationships between wheat yields and fertilizer rates in southern Australia[J]. Aust J of Soil Res, 1984, 22: 191-205. |
 2014, Vol. 31
2014, Vol. 31