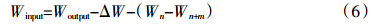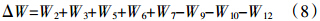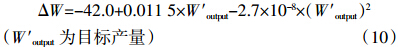文章信息
- 黄治平, 米长虹, 侯彦林, 刘书田, 郑宏艳, 王农, 蔡彦明, 王铄今, 侯显达
- HUANG Zhi-ping, MI Chang-hong, HOU Yan-lin, LIU Shu-tian, ZHENG Hong-yan, WANG Nong, CAI Yan-ming, WANG Shuo-jin, HOU Xian-da
- 生态平衡施肥模型与目标产量施肥模型比较研究
- Comparison of Target Yield Method and Ecological Balanced Fertilization Model
- 农业资源与环境学报, 2014, 31(6): 495-499
- Journal of Agricultural Resources and Environment, 2014, 31(6): 513-520
- http://dx.doi.org/10.13254/j.jare.2014.0287
-
文章历史
- 收稿日期:2014-10-23
2. 北京农业信息技术研究中心, 北京 100089;
3. 北京优雅施软件研发服务中心, 北京 100089
2. Beijing Research Center for Information Technology in Agriculture, Beijing 100089, China;
3. Software Development and Service Center of Beijing Yours, Beijing 100089, China
施肥模型主要分为两大类,一类是肥料效应函数模型,属于统计模型,被广泛应用,并有逐渐发展成与测土推荐施肥模型相结合的趋势[1, 2];另一类是测土推荐施肥模型,属于平衡模型,目标产量施肥模型是测土推荐施肥模型中的典型代表,目前仍作为主要施肥模型在国内外广泛应用[3, 4],从表面上看模型构造无可争议,但在应用上存在诸多弊端也是公认的事实[5, 6, 7, 8, 9, 10, 11, 12]。
目标产量施肥模型和主要参数计算公式如公式(1)所示。
式中:Winput为施肥量(kg·hm-2);Woutput为作物产量需要的养分量(kg·hm-2);ksoil为土壤有效养分(表观)利用率(%);Tn为土壤有效养分测定值(mg·kg-1);kfer为肥料养分(当季)利用率(%);2.25为将土测值换算为kg·hm-2的平均乘数,这里每公顷20 cm耕层按225万kg土壤计算。
目标产量施肥模型参数主要存在以下问题:土壤有效养分供应量、特别是土壤供氮量的测定,是迄今测土法研究中尚未解决的难题;所使用的土壤有效养分利用率和肥料养分利用率这两个参数是相互影响的变量,不是常数,有充分的研究证据表明,土壤有效养分测定值与土壤有效养分利用率呈显著负相关,与土壤供应量呈对数曲线关系,与当季肥料养分利用率呈负相关[7, 8, 9];参数的求得建立在缺素区土壤有效养分供应量基础上,而缺素区和施肥区的土壤有效养分供应量明显有别,一些研究表明,激发效应造成施肥区土壤N平均利用率增加5%以上[10],因此,用试验条件下缺素区土壤有效养分供应量代替试验条件下施肥区土壤有效养分供应量而去预测其他地块的施肥量显然不妥;在确定施肥量时,耕层一季养分矿化或释放量是被折算在耕层有效养分含量之中计算的,且所指土壤供应量只限于耕层土壤,因此土壤有效养分利用率有时高达100%以上,故有时也称为“表观利用率”。上述诸多原因使目标产量施肥模型难以作为精确预测施肥量的模型而使用。
以下通过具体数字分析,对目标产量施肥模型预测精度进行定量评价。表 1是基于吉林省近年大面积玉米肥料田间试验平均经济施肥量而对目标产量施肥模型参数进行拟合的结果。其中,玉米百公斤籽粒需氮量按2.5 kg(高产品种如吉单209)计算,式中2.25×Wn×ksoil的具体数值相当于玉米产量养分需要量的百分数,这部分由土壤提供。表 1的核心内容是在田间试验获得经济施肥量的前提下,模拟求算相匹配的目标产量施肥模型参数组合,目的是通过反证法证明任何一个经济施肥量对应着无数个参数组合,而通常一个确定的田间试验所求得的只不过是其中的一个组合而已。
例如:预测11 250 kg·hm-2产量时的施肥量,需氮量281.3 kg·hm-2,土壤供氮量按225(281.3×0.8)kg·hm-2计算,则需氮为56.3÷0.28(肥料利用率%)=201.1 kg·hm-2。如果土壤有效氮含量为120 mg·kg-1,则其利用率必须为83%时,才能提供225 N kg·hm-2(120×2.25×0.83=224.1);如果土壤有效氮含量为100 mg·kg-1,则其利用率必须为100%时,才能提供225 N kg·hm-2;如果土壤有效氮含量为80 mg·kg-1,则其利用率必须为125%时,才能提供225 N kg·hm-2。如果将土壤有效氮利用率定为83%,产量定为11 250 kg·hm-2,需氮量为281.3 kg·hm-2,肥料利用率定为28%,则土壤有效氮含量分别为125、120、115 mg·kg-1时,施氮量分别为170.9、204.3、237.6 kg·hm-2。土壤有效氮测定足以造成5 mg·kg-1误差,而5 mg·kg-1有效氮含量之差绝不应当造成施肥量预测如此大的差异;土壤有效养分利用率和肥料养分利用率是通过田间试验取得的施肥参数,并且是以不施肥区或缺素区作为对照求得的,这些参数在用于施肥区时条件已经发生变化,因此,两个最重要的施肥参数必将发生变化,除此之外的任何其他影响因素也都有可能使这两个施肥参数分别产生5%以上的误差,从表 1 中可以看出,5%利用率误差足以使施肥量预测失真。
 |
以上分析结果说明,目标产量施肥模型预测精度有限,其根源在于方法本身参数多,参数易变,参数准确测定困难,参数间存在相互影响关系等等。
在实际应用目标产量模型预测(经济)施肥量时,常常将地块划分为高、中、低不同的肥力等级,不同的肥力等级施肥参数不同,生产实践中地块肥力等级是相对的,不可能有明确的自然属性作为划分标准。而对于一个具体地块而言,在应用不同肥力等级施肥参数进行预测时,由于施肥参数的不连续性,结果必将产生显著不同的施肥量预测结果,而一个具体的地块只能接受一个预测结果。科学的施肥模型,即使使用不同肥力等级的施肥参数进行预测,如果提供的地块信息完全相同,应当得到相同或非常近似的数值,否则,难以评价哪一个肥力等级的施肥参数是正确的。当然,实际应用中可以将施肥参数划分为无穷等级(微分学思想),使参数近似连续,但在操作上很难实现。当考虑到土壤有效养分利用率时,情况就更加复杂。以表 1为例,当Winput=144 kg·hm-2,2.25×Wn-×ksoil=75%×187.5=141 kg·hm-2,kfer=32%,这时W'input=144 kg·hm-2。表 2说明同一土壤有效养分供应量同样对应着无数个土壤有效养分含量和土壤有效养分利用率的解。
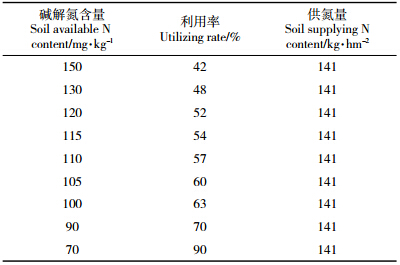 |
从表 1可以明确地看出,一个确定的经济施肥量对应着由多个参数组成(如至少为ksoil、kfer)的无数个解,这些参数之间存在着错综复杂的相互作用关系,因此,很难确定真正的参数解。即使通过肥料田间试验能够确定参数的真正解,其实它也只是一个不稳定的解,一旦某些参数发生变化,其他参数将随之而变,确定变化后的参数的真正解是十分困难的。因此,施肥量预测难以准确。同时,目标产量施肥模型的主要参数均是以无肥区或缺素区作为对照求得的,将其应用在与获得参数条件不同的施肥区时这些参数必将发生变化,即施肥区和不施肥区土壤有效养分利用率显然不同,由此可以想象出参数的可信程度。目标产量模型参数解就像是通过圆心的一条射线,它与圆周的交点处就是某一组参数(由产量、土壤有效养分利用率、肥料养分利用率等组成)所确定的经济施肥量,而通过该点的法线方程就像是施肥量预测方程,法线与射线相交处即为预测施肥量,此时此点是试验结果或参数调整的结果,因此必然落在圆周上。当任何参数之一发生变化时,穿过圆心的射线将发生移动,移动某个角度后的射线仍然与圆周相交,相交点即为新的经济施肥量,但是如果再利用原法线预测经济施肥量,这时法线与射线的相交点必将在圆外,射线移动的角度越大(与调整好参数时的产量之差越大),预测施肥量误差越大。所以,只有获得法线随射线移动的变化规律,及时给出新的法线方程才能准确地预测经济施肥量,这将是耗费巨大人力、物力、财力和相当时间的工作,而且研究结果的适用性也有待评价。从严格理论意义上讲,目标产量施肥模型表面看上去是平衡模型,但它只不过是以作物为核心来调整施肥量以达到预期产量的平衡帐,并没有考虑土壤养分是否平衡。生态平衡施肥要求施肥技术同时能够兼顾提高产量、改善品质、减低成本、培肥土壤、减少污染的多重任务[12],显然,目标产量施肥模型即便是在理论上也不能满足新时代的要求,何况其施肥参数还存在诸多弊端。除非我们能够通过肥料田间试验准确求出下列方程(4)和方程(5),否则,目标产量施肥模型难以达到准确预测施肥量的目的。
2 生态平衡施肥模型应用实例生态平衡(通用)施肥模型通用表达式为[12]:
即
其中,
即
由式(6)可知,在保持现有肥力水平不变的条件下,(Wn-Wn+m)≈0。于是,Winput=Woutput-ΔW。应用近年吉林省玉米平衡施肥多点试验结果,获得玉米区域性经济施氮模型如公式(10)和公式(11)。ΔW方程建立的方法如下:以某肥料田间试验条件下所获得的最佳产量作为W′output,然后将其转换成Woutput(产量需要的养分量),再由ΔW=Woutput-Winput求出与最佳产量W′output相对应的ΔW,并将其作为因变量,最后建立自变量(W′output)与因变量(ΔW)的相关关系,根据拟合情况确定模型表达方式。
应用公式(10)和公式(11)可以预测不同玉米目标产量条件下的区域性施氮量。例如:某地块根据目前平年产量和肥力状况,设定目标产量为12 000 kg·hm-2,则施肥量计算过程如下:Winput=42.0+0.013 5×12 000+2.7×10-8×(12 000)2=207.8 N (kg·hm-2)
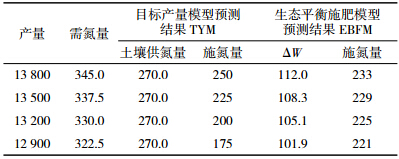
在13 500 kg·hm-2产量附近时,设土壤有效氮(碱解氮)含量为140 mg·kg-1,土壤有效氮利用率为86%,肥料利用率为30%,利用生态平衡施肥模型和目标产量施肥模型预测结果见表 3。用目标产量施肥模型预测时,在13 500 kg·hm-2产量时获得试验参数或调整好参数,当产量偏离300、600 kg·hm-2时,施氮量相差25、50 kg·hm-2,而这时需氮变幅仅为7.5、15 kg·hm-2;用生态平衡施肥模型预测时,产量相差300 kg时,需氮量变幅7.5 kg·hm-2,施肥量变幅为4 kg·hm-2,其余由土壤(实际为ΔW)提供。当然目标产量模型也可以通过调整参数组合而实现精确预测施肥量的目的,但如何调整土壤有效养分利用率、肥料养分利用率以及不同土壤有效养分含量条件下的供肥量是极其复杂的,必须通过大量的肥料田间试验才能获得这些参数的变化规律及其相互关系[7, 8, 9],实属“事倍功半”的工作。
 |
生态平衡施肥模型是通用机理模型[12]。我们在内蒙古赤峰市元宝山区经过2年多点肥料田间试验和总结分析吉林省近年肥料田间试验数据,发现它与目标产量施肥模型相比,具有诸多优点,而肥料效应函数模型是它的特例。因此,生态平衡施肥模型具有目前两大类施肥模型的双重功能,在施肥模型研究上具有重要的理论和实践意义。
3 结论目标产量施肥模型在20世纪科学施肥实践中发挥了积极作用,其模型构造看上去完全合理,施肥参数获得方法也不难,但施肥参数的可信程度越来越值得质疑。用缺素区作为参照求得的施肥参数用于预测施肥区的施肥量,这一点本质上缺乏科学性;两个主要施肥参数即两个“百分率”参数不是常数,而且存在相互依赖和影响关系,难以适应实践需求;没有考虑到土壤有效养分平衡或变化,缺乏生态环境学意义和可持续土地利用思想。因此,它难以作为精确施肥模型使用。与其相比,生态平衡施肥模型将施肥系统中诸多变量统一在质量守恒定律之下,具有测土施肥模型和肥料效应函数模型的双重功能,参数变异小,参数易于获得和预测施肥量准确等诸多优点,但作为一类新型模型,有必要从理论、方法和应用效果上对其进行系统研究和评价。
| [1] | Ghosh P C, Misra U K. Modified Mitscherlich-Bray equation for calculation of crop response to applied phosphmte[J]. Journal of the Indian Society of Soil Science,1996, 44(4): 786-788. |
| [2] | Bangar A R. Fertilization of sorghum based on modified Mitscherlich-Bray equation under semi-arid tropics[J]. Journal of the Indian Society of Soil Science, 1998, 46(3): 383-391. |
| [3] | Prasad R, Prasad B. Fertilizer requirements for specific yield targets of soybean based on soil testing in alfisols[J]. Journal of the Indian Society of Soil Science, 1996, 44(2): 332-333. |
| [4] | Katsuyuki Katayama, Osamu Ito, Joseph Jackson Adu-Gyamfi, et al. Effects of NPK fertilizer combinations on yield and nitrogen balance in sorghum or pigeonpea on a vertisol in the semi-arid tropics[J]. Soil Sci Plant Nutr, 1999, 45(1): 143-150. |
| [5] | 农牧渔业部农业局. 配方施肥技术工作要点[J]. 土壤肥料, 1987(1): 6-12.Ministry of Agriculture Animal Husbandry and Fisheries Bureau of Agriculture. Working outline recommended fertilization technology[J]. Soils and Fertilizers, 1987(1): 6-12.(in Chinese) |
| [6] | 金耀青. 配方施肥的方法及其功能[J].土壤通报, 1989, 20(1): 46-49.JIN Yao-qing. The method and function of recommended fertilization[J]. Chinese Journal of Soil Science, 1989, 20(1): 46-49.(in Chinese) |
| [7] | 刘文通, 刘声元, 郝景发. 长春地区诊断施肥量计算公式中几个参数的探讨[J]. 土壤通报, 1984, 15(3): 117-120.LIU Wen-tong, LIU Sheng-yuan, HAO Jing-fa. Study on several parameters of calculation formula diagnosis fertilizer rate in Changchun area[J]. Chinese Journal of Soil Science, 1984, 15(3): 117-120.(in Chinese) |
| [8] | 张 宽, 赵景云, 王秀芳, 等. 黑土供磷能力与磷肥经济合理用量问题的初步研究[J]. 土壤通报, 1984, 15(3): 120-123.ZHANG Kuan, ZHAO Jing-yun, WANG Xiu-fang, et al. A preliminary study on phosphorus supply capacity and phosphate fertilizer economic reasonable amount in black soil[J]. Chinese Journal of Soil Science, 1984, 15(3): 120-123.(in Chinese) |
| [9] | 姜文彬, 杨铁成, 单文波. 玉米诊断施肥技术的研究与应用[J]. 吉林农业大学学报, 1986, 8(4): 62-68.JIANG Wen-bin, YANG Tie-cheng, SHAN Wen-bo. Research and application on corn diagnosis fertilization technique[J]. Journal of Jilin Agricultural University, 1986, 8(4): 62-68.(in Chinese) |
| [10] | 周鸣铮, 王竺美. 浙江省水稻土“因产定氮”基本公式极其有关参数的探讨[J]. 土壤学报, 1987, 24(2): 127-133.ZHOU Ming-zheng, WANG Zhu-mei. Studies on new equations and its parameters for calculation of the requirement of nitrogen according to the maximum yield of rice predicted[J]. Acta Pedologica Sinica, 1987, 24(2): 127-133.(in Chinese) |
| [11] | 侯彦林, 刘兆荣. 生态平衡施肥模型理论与应用[J]. 土壤通报, 2000, 31(1): 33-35.HOU Yan-lin, LIU Zhao-rong. Theory and application of ecological balanced fertilization model[J]. Chinese Journal of Soil Science, 2000, 31(1): 33-35.(in Chinese) |
| [12] | 侯彦林. “生态平衡施肥”的理论基础和技术体系[J]. 生态学报, 2000, 20(4): 133-139.HOU Yan-lin. Theory and technological system of ecological balanced fertilization[J]. Acta Ecologica Sinica, 2000, 20(4): 133-139.(in Chinese) |
 2014, Vol. 31
2014, Vol. 31